Mixture Models and EM

How to model data with a probability distribution? For example, if data looks like a circle or symmetric, we may model it with a Gaussian distribution:

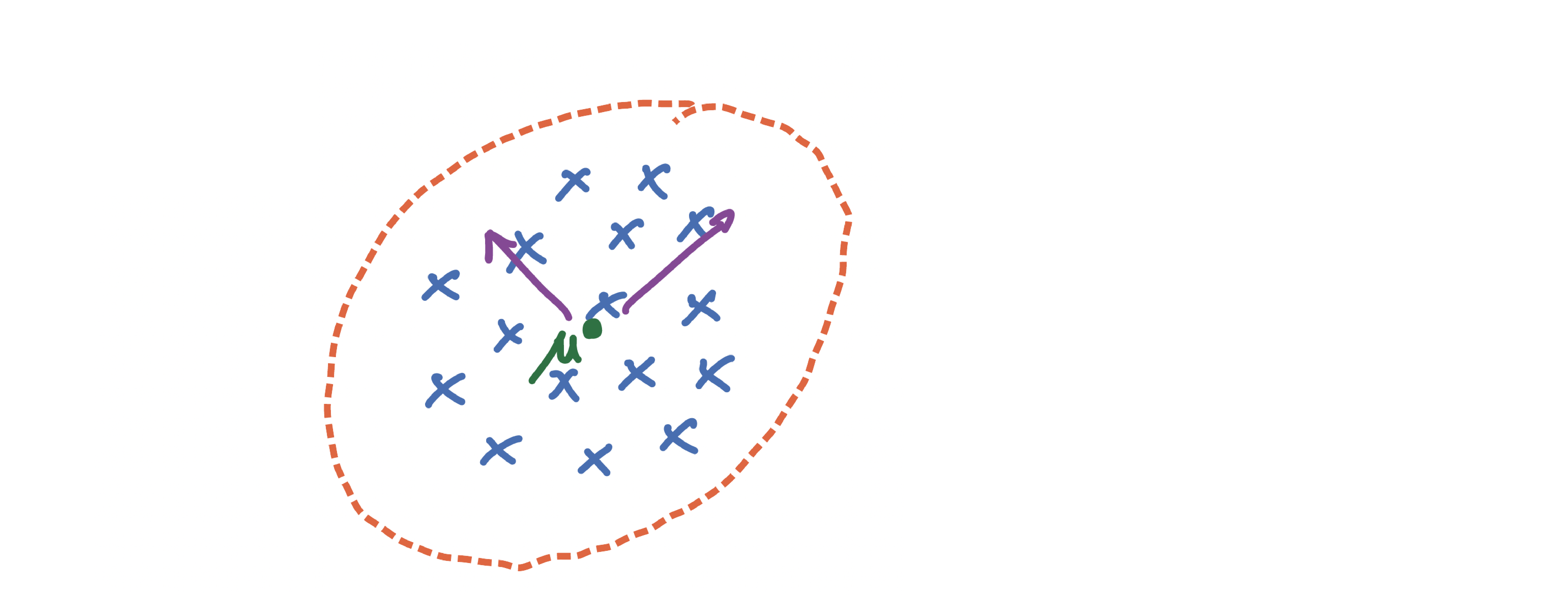
With the following density function:

$$\text{Normal}(\mu ,\mathrm{\Sigma })=\frac{\exp (-\frac{1}{2}(x-\mu {)}^T{\mathrm{\Sigma }}^{-1}(x-\mu ))}{(2\pi {)}^{\frac{d}{2}}\sqrt{\text{det}\mathrm{\Sigma }}}$$

Given i.i.d data points $x_1$, $x_2$, .., $x_n \sim \text{Normal}(x|\mu^,\Sigma^)$, maximum likelihood estimator is:

$$\begin{array}{r}\begin{array}{rl}\text{MLE}(\mu ,\mathrm{\Sigma })=& \arg max\prod _{i=1}^n\text{Normal}(x_i|\mu ,\mathrm{\Sigma })\\ =& \arg min-\sum _{i=1}^n\log \text{Normal}(x_i|\mu ,\mathrm{\Sigma })\\ =& \arg min\sum _{i=1}^n\frac{1}{2}(x-\mu {)}^T{\mathrm{\Sigma }}^{-1}(x-\mu )+\frac{1}{2}\log \text{det}\mathrm{\Sigma }+\frac{d}{2}\log 2\pi \end{array}\end{array}$$

The solution is:

$$\begin{array}{r}\begin{array}{rl}{\mu }_{\text{MLE}}=& \frac{1}{n}\sum _{i=1}^n{x}_i=\overline{x}\\ {\mathrm{\Sigma }}_{\text{MLE}}=& \frac{1}{n}\sum _{i=1}^n(x_i-{\mu }_{\text{MLE}})(x_i-{\mu }_{\text{MLE}}{)}^T\end{array}\end{array}$$

But how about data that looks like this?

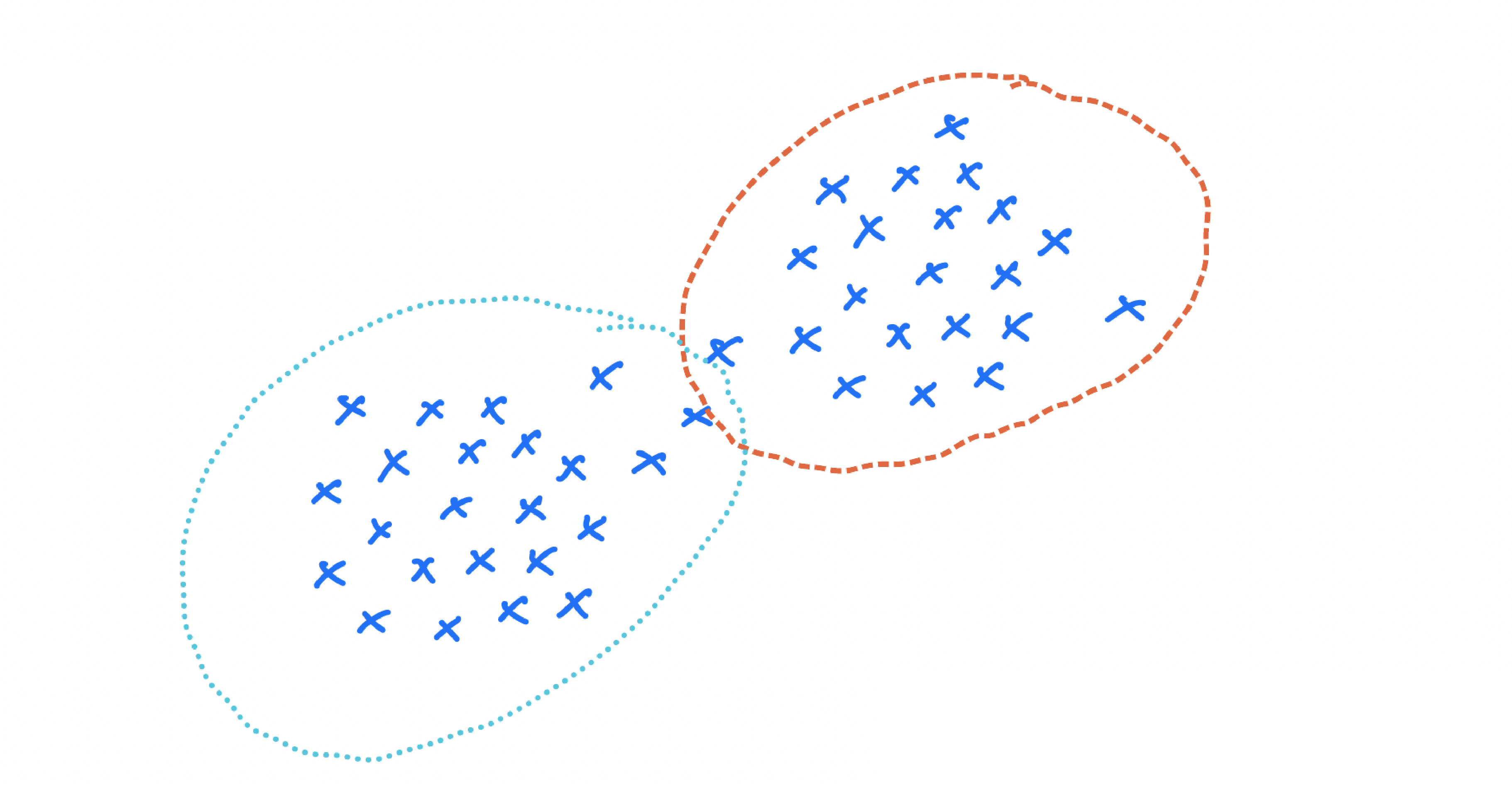
Here, Gaussian could be a better model, and we can not fit a multi-modal Gaussian. One solution is a mixture of Gaussian:

$$p(x)={\pi }_1\text{Normal}(x|{\mu }_1,{\mathrm{\Sigma }}_1)+..+{\pi }_k\text{Normal}(x|{\mu }_k,{\mathrm{\Sigma }}_k)$$

The following plot is an example of a Gaussian mixture distribution in one dimension showing three Gaussians (each scaled by a coefficient) in blue and their sum in red.

$$\begin{array}{r}\begin{array}{c}p(x)={\pi }_1\text{Normal}(x|{\mu }_1,{\sigma }_1^2)+{\pi }_2\text{Normal}(x|{\mu }_2,{\sigma }_2^2)+{\pi }_3\text{Normal}(x|{\mu }_3,{\sigma }_3^2),\\ {\pi }_1+{\pi }_2+{\pi }_3=1,\\ {\pi }_1,{\pi }_2,{\pi }_3\ge 0.\end{array}\end{array}$$

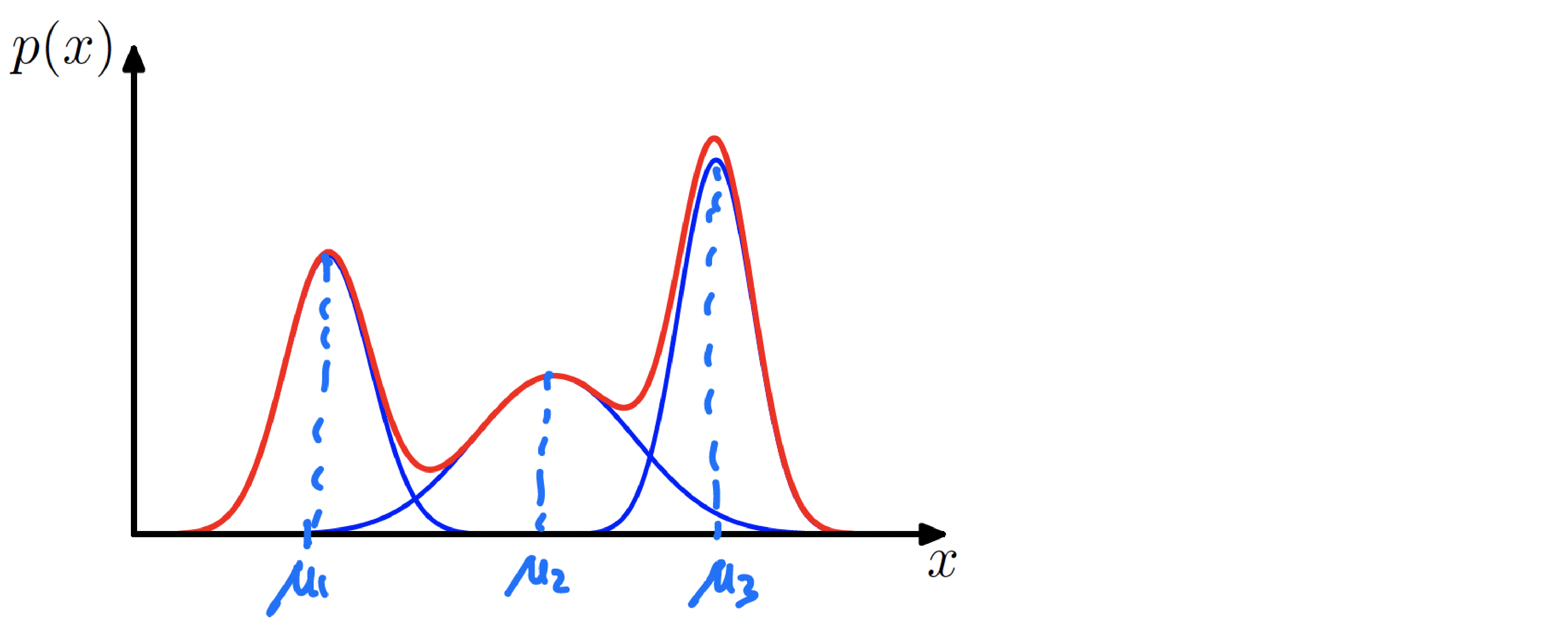
Mixture of Gaussian with $K$ components

Let’s formalize a mixture of the Gaussian model:

$$p(x)=\sum _{i=1}^K{\pi }_k\text{Normal}(x|{\mu }_k,{\mathrm{\Sigma }}_k)$$

define $z\in (0,1{)}^k$ to encode which component $x$ comes from: $z=(z_1,z_2,..,z_k)$ and $z_k\in (0,1)$ and $z_1+..+z_k=1$. Or in other words:

$$z\in e_1=\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right),e_2=\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right),e_3=\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$$

Graphical model:

$$p(x,z)=p(z).p(x|z)$$

1. define marginal on $z$:

$$p(z_k=1)={\pi }_k\text{for}1\le k\le K$$

where $\pi =({\pi }_1,..,{\pi }_k)$ satisfies $0\le p{i}_k\le 1$, $\sum _{k=1}^K{\pi }_k=1$. Because $z=(z_1,..,z_k)\in (0,1{)}^k$ we can write the following equation:

$$p(z)=\prod _{k=1}^K{\pi }_k^{z_k}$$

since only one $z_k=1$ and all $z_j=0,j\ne k$.

2. define conditional:

$$\begin{array}{r}p(x|z_k=1)=\text{Normal}(x|{\mu }_k,{\mathrm{\Sigma }}_k)\\ p(x|z)=\prod _{k=1}^K\text{Normal}(x|{\mu }_k,{\mathrm{\Sigma }}_k{)}^{z_k}\end{array}$$

3. define joint probability:

$$\begin{array}{rl}p(x,z)=& p(z).p(x|z)\\ =& \prod _{k=1}^K({\pi }_k\text{Normal}(x|{\mu }_k,{\mathrm{\Sigma }}_k){)}^{z_k}\end{array}$$

or $p(x,z_k=1)={\pi }_k\text{Normal}(x|{\mu }_k,{\mathrm{\Sigma }}_k)$

4. marginal is a mixture of Gaussian:

$$p(x)=\sum _{z}p(x,z)=\sum _{k=1}^{K}p(x,z_k=1)={\pi }_k\text{Normal}(x|{\mu }_k,{\mathrm{\Sigma }}_k)$$

Therefore to sample from a mixture of Gaussian:

$$p(x)=\sum _k{\pi }_k\text{Normal}(x|{\mu }_k,{\mathrm{\Sigma }}_k)$$

We can do the following:

• draw a sample $z\sim p(z)$, so with probability ${\pi }_k$, we are in $k-$th component.
• given $z_k=1$ draw : $x|z_k=1\sim \text{Normal}(x|{\mu }_k,{\mathrm{\Sigma }}_k)$

If we think of $p(z_k=1)={\pi }_k$ as prior, then given $x$, we can compute posterior distribution:

$$\begin{array}{rl}\gamma (z_k)=& p(z_k=1|x)\\ =& \frac{p(z_k=1).p(x|z_k=1)}{\sum _{i=1}^{K}p(z_j=1).p(x|z_j=1)}\\ =& \frac{{\pi }_k.\text{Normal}(x|{\mu }_k,{\mathrm{\Sigma }}_k)}{\sum _{i=1}^K{\pi }_j.\text{Normal}(x|{\mu }_j,{\mathrm{\Sigma }}_j)}\end{array}$$

Maximum Likelihood Estimation for Gaussian Mixture

Given observations $x_1,x_2,..x_N\in R^d$, we want to model using mixture of $K$ Gaussian (for a fixed $K$):

$$p(x)=\sum _k{\pi }_k\text{Normal}(x|{\mu }_k,{\mathrm{\Sigma }}_k)$$

for each $x_n\in R^d$ define latent variable $z_n\in (0,1{)}^k$:

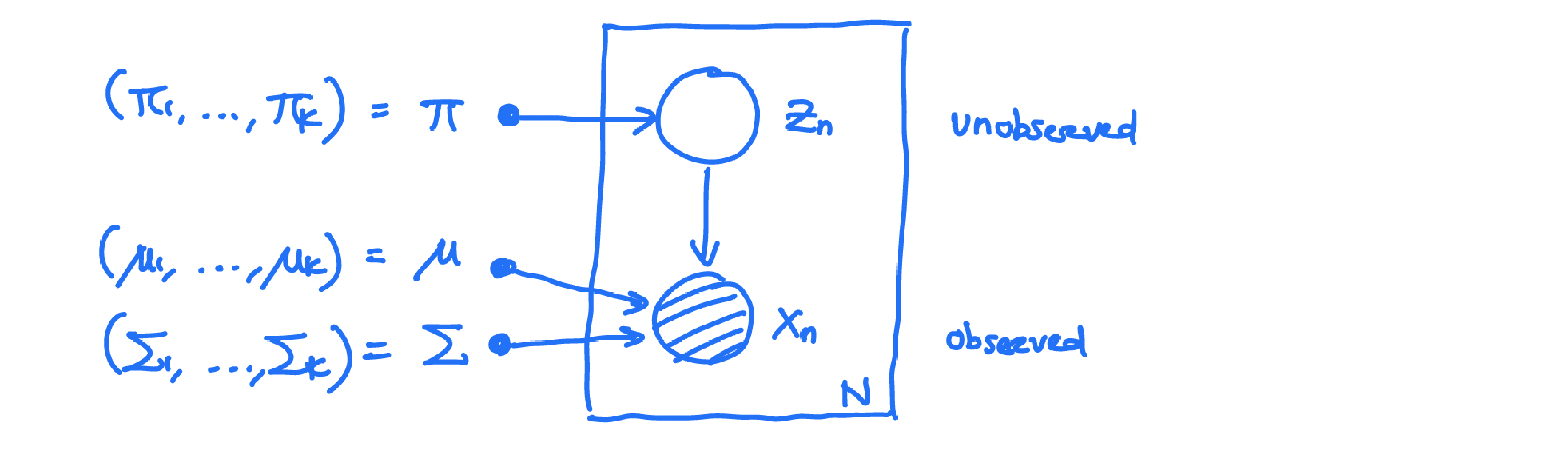
joint probability for $x=(x_1,..,x_N)$ is defined as:

$$\begin{array}{rl}p(x)=& \prod _{n=1}^{N}p(x_n)\\ =& \prod _{n=1}^N(\sum _k{\pi }_k\text{Normal}(x|{\mu }_k,{\mathrm{\Sigma }}_k))\end{array}$$

based on MLE estimator: $\pi =({\pi }_1,..{\pi }_k)$ , $\mu =({\mu }_1,..{\mu }_k)$ , $\sigma =({\mathrm{\Sigma }}_1,..{\mathrm{\Sigma }}_k)$ to maximize log-likelihood :

$$\begin{array}{rl}\log p(x)=& \sum _{i=1}^N\log (\sum _k{\pi }_k\text{Normal}(x|{\mu }_k,{\mathrm{\Sigma }}_k))\\ =& \sum _{i=1}^N\frac{\exp (-\frac{1}{2}(x-\mu {)}^T{\mathrm{\Sigma }}^{-1}(x-\mu ))}{(2\pi {)}^{\frac{d}{2}}\sqrt{\text{det}\mathrm{\Sigma }}}\end{array}$$

1. suppose we fix $\pi =({\pi }_1,..,{\pi }_k)$ , $\mathrm{\Sigma }=({\mathrm{\Sigma }}_1,..,{\mathrm{\Sigma }}_k)$, then we can optimize over $\mu =({\mu }_1,..,{\mu }_k)$:

$$\begin{array}{rl}\frac{\partial }{\partial {\mu }_k}\log p(x)=& \sum _{i=1}^N\frac{{\pi }_k\text{Normal}(x_n|{\mu }_k,{\mathrm{\Sigma }}_k)}{\sum _{j=1}^K\text{Normal}(x_n|{\mu }_j,{\mathrm{\Sigma }}_j}.{\mathrm{\Sigma }}_k^{-1}(x_n-{\mu }_k)\\ \end{array}$$

where $\sum _{j=1}^K\text{Normal}(x_n|{\mu }_j,{\mathrm{\Sigma }}_j)=\gamma (z_{nk})=p(z_{nk}=1|x_n)$. $$\begin{array}{r}\frac{\partial }{\partial {\mu }_k}\log p(x)=({\mathrm{\Sigma }}_k{)}^{-1}\sum _{n=1}^N\gamma (z_{nk})(x_n-{\mu }_k)\end{array}$$

To find a minimizer, set the gradient to $0$: $$\begin{array}{r}{\mu }_k=\frac{1}{N_k}\sum _{n=1}^N\gamma (z_{nk})x_n\end{array}$$ which is weighted average data points where $N_k=\sum _{n=1}^N\gamma (z_{nk})$ is efficient number of data points assigned to cluster $k$.

2. Similarly, if we fix $\mu ,\pi$ we can optimize over $\mathrm{\Sigma }$:

$$\begin{array}{r}{\mathrm{\Sigma }}_k=\frac{1}{N_k}\sum _{n=1}^N\gamma (z_{nk})(x_n-{\mu }_k)(x_n-{\mu }_k{)}^T\end{array}$$

3. If we fix $\mu ,\mathrm{\Sigma }$ we can then optimize over $\pi$:

$${\pi }_k=\frac{N_k}{N}$$

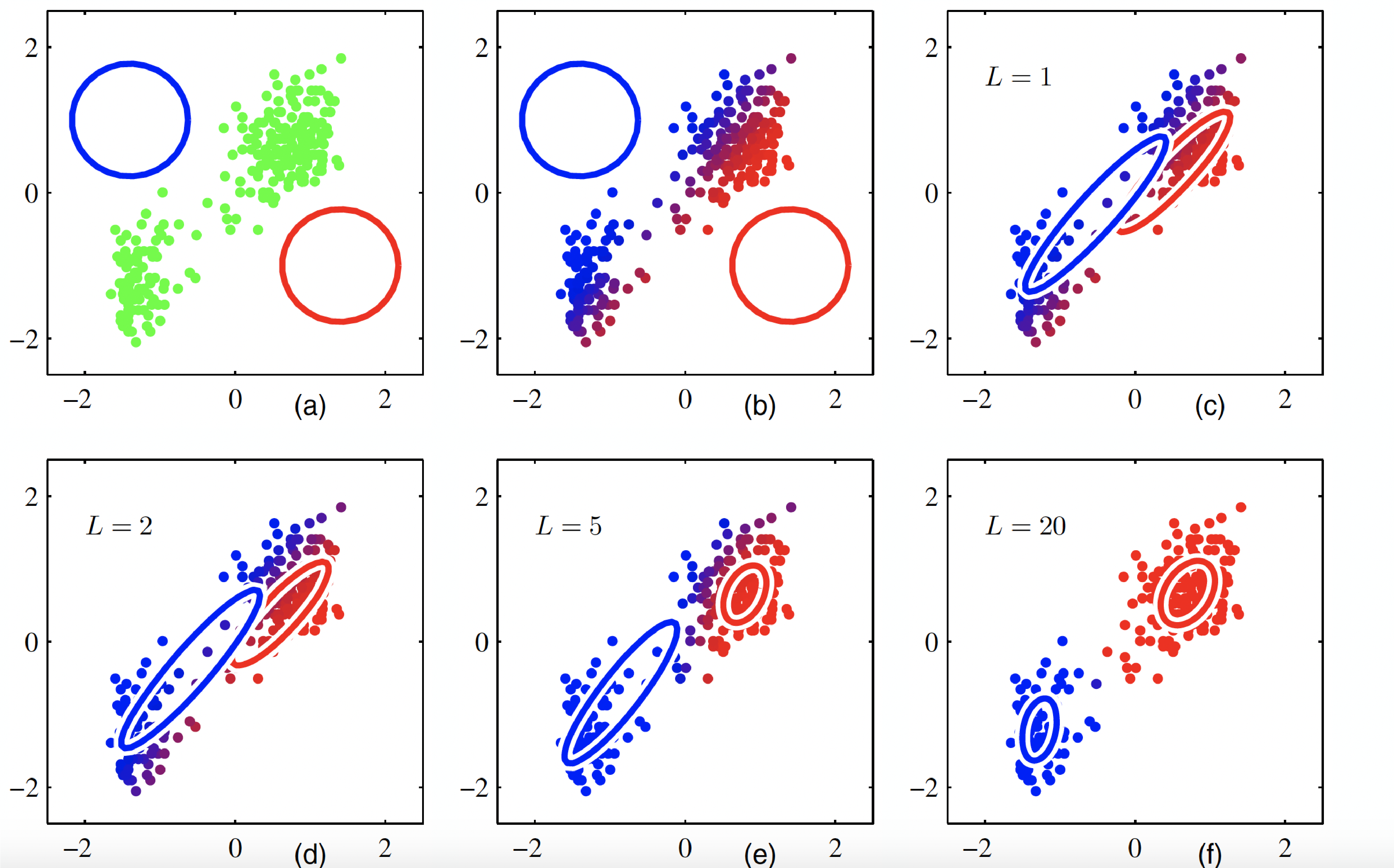
The following plot illustrates the EM algorithm (Bishop Fig. 9.8).

We covered this post in the introduction to machine learning CPCS 481/581, Yale University, Andre Wibisono where I (joint with Siddharth Mitra) was TF.